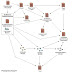
La idea del algoritmo es que a través de las iteraciones construyamos dos partes diferenciadas con los elementos que tenemos que ordenar: una parte ordenada y una parte desordenada. Conforme pasan las iteraciones, iremos agregando elementos a la parte ordenada con elementos de la parte desordenada, hasta que la parte desordenada se quede sin elementos y nuestra parte ordenada sea el resultado del algoritmo. Imaginemos que estamos aplicando el Ordenamiento por Inserción para alinear un filar de personas por orden de talla. En una iteración intermedia, tendríamos este escenario:
El algoritmo ya ha hecho su trabajo y nos ha dividido al grupo de personas en dos partes: una ordenada y una que tenemos que ordenar. Lo que se hace en cada iteración es tomar al primer elemento de la izquierda de la parte desordenada (en el gráfico "Marked player") para colocarlo en lista ordenada en el lugar que le corresponda. Entonces, sacamos a "Marked player" de la fila para ver donde lo colocamos.
Ahora la parte de la izquierda-que estaba ordenada- ha crecido en una persona y la parte desordenada de la derecha es una persona menor. Es momento de escoger un nuevo "Marked player" tomando a la primera persona de la izquierda de la lista desordenada. Repetimos el proceso tres veces más y hemos terminado.
Si en vez de un grupo de personas utilizamos un arreglo de enteros, el programa Java para ordenarlos mediante ordenamiento por inserción sería más o menos así:
public void insertionSort() {
int in, out;
for (out = 1; out < nElems; out++) {
long temp = a[out];
in = out;
while (in > 0 && a[in - 1] >= temp) {
a[in] = a[in - 1];
--in;
}
a[in] = temp;
}
}
Cuyo proceso es más o menos el que sigue:
- La variable nElems contiene la longitud del arreglo a[] que vamos a ordenar. La variable out la utilizamos para marcar el inicio de la porción no ordenada del arreglo. Nuestra parte ordenada al incio del algoritmo será el primer elemento de a[] (o sea a[0]) y la parte desordenada comenzará en a[1]; es por eso que la variable out se inicializa en 1: esta variable nos marcará siempre el inicio de la parte desordenada del arreglo.
- Colocamos el valor de a[out] (nuestro "Marked player") en la variable temp, dado que al desplazar los elementos de la parte ordenada hacia la derecha podríamos perder su valor.
- Inicializamos la variable in con el valor de out, y utilizaremos esta variable para desplazarnos a lo largo de la parte ordenada con el fin de encontrar el lugar que le corresponde a a[out] en la parte ordenada del arreglo. Para esto, comparamos si a[i-1] es mayor que el valor de a[out] almacenado en temp. Si es así, desplazamos a[i-1] a la derecha, y disminuimos i en una unidad para seguir recorriendo la parte ordenada del arreglo.
- Cuando a[i-1] sea menor que temp -que contiene a[out]- es que hemos encontrado al fin el lugar que le correspode a nuestro "Marked Player". El valor de a[out] ahora estará almacenado en a[i], y estamos listos para tomar el siguiente elemento de la parte desordenada del arreglo.
Como en el post anterior, nos toca determinar cúantos pasos le toma a nuestro algoritmo ordenar un arreglo arbitrario de longitud N, en el peor escenario posible (la gente de algoritmos siempre es pesimista). En la primera iteración, la parte ordenada tiene sólo un elemento, así que a lo más realizaríamos una comparación al ordenar. En la segunda iteración, como ya tendríamos dos elementos en la parte ordenada el algoritmo realizaría como máximo dos comparaciones; y en la última iteración, sólo nos quedaría realizar N-1 comparaciones en el peor escenario posible. Si sumamos todas las comparaciones, tendríamos:
1 + 2 + 3 + ... + N - 1 = N*(N-1)/2
*De acuerdo a la fórmula que enseñan en secundaria
El tiempo de ejecución del algoritmo es proporcional al número de pasos; por lo que el tiempo de ejecución del algoritmo de ordenamiento por inserción para un arreglo de longitud N es proporcional a N al cuadrado.
Código fuente e imágenes tomadas de Data Structures and Algorithms in Java.















1 comments:
Estoy aprendiendo esto de algoritmos en la universidad , me ha ayudado mucho esta explicacion .
Replygracias.
Publicar un comentario